Lattice gauge theories at finite fermion density
Lattice gauge theories are ubiquitous in physics, describing a wide range of phenomena from quark confinement in high energy physics to the low energy effective theories of exotic quantum materials such as spin liquids and doped Mott insulators. At finite fermion density, lattice gauge theories are notoriously difficult to analyze due to the fermion sign problem, which renders quantum Monte Carlo simulations uncontrolled with a statistical noise that overwhelms the data.
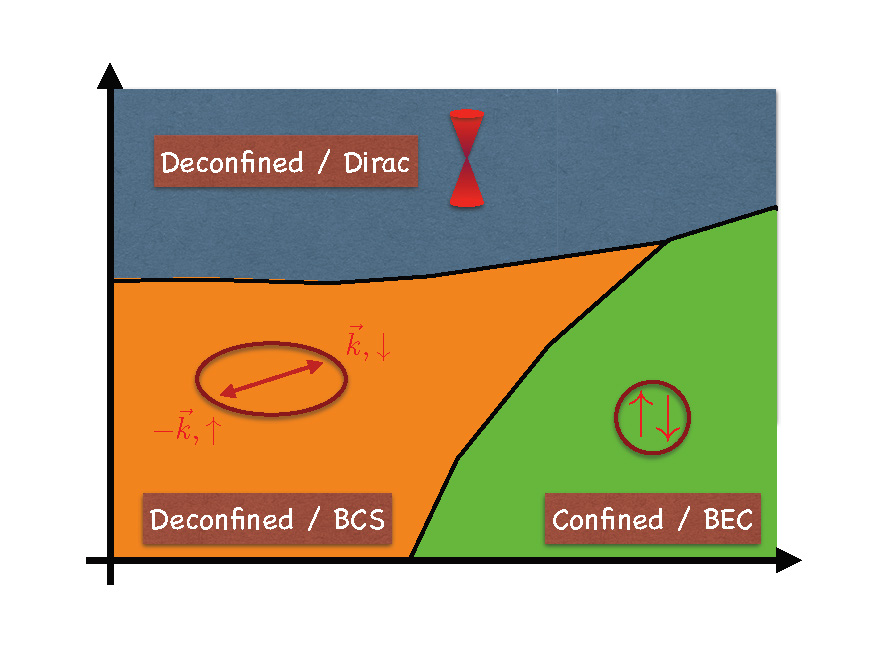
In a recent work, we have made substantial progress in the solution of the numerical sign-problem for the Ising gauge theory [S. Gazit et al. Nature Physics (2017)], a model of great interest in condensed matter physics and a paradigmatic example of topological order. Circumventing the sign-problem allowed us to elucidate the phase diagram at arbitrary fermion density in a numerically unbiased manner.
We have uncovered a rich phase diagram hosting exotic phases of matter. In particular, we have found that strong interactions between gauge fields and fermions lead to the emergence of Dirac particles which provide a non-trivial example for violation of Luttinger’s theorem due to fractionalization. Unexpectedly, our numerical results indicate that the appearance of Dirac fermions is accompanied by an unconventional quantum critical point that can not be described by the standard Landau theory of phase transitions [S. Gazit et al. PNAS (2018)]. We have developed a novel field theoretical understanding of the transition, which involves a deconfined critical point with emergent and enlarged local (gauge) and global symmetries.
Topological phases in periodically driven systems
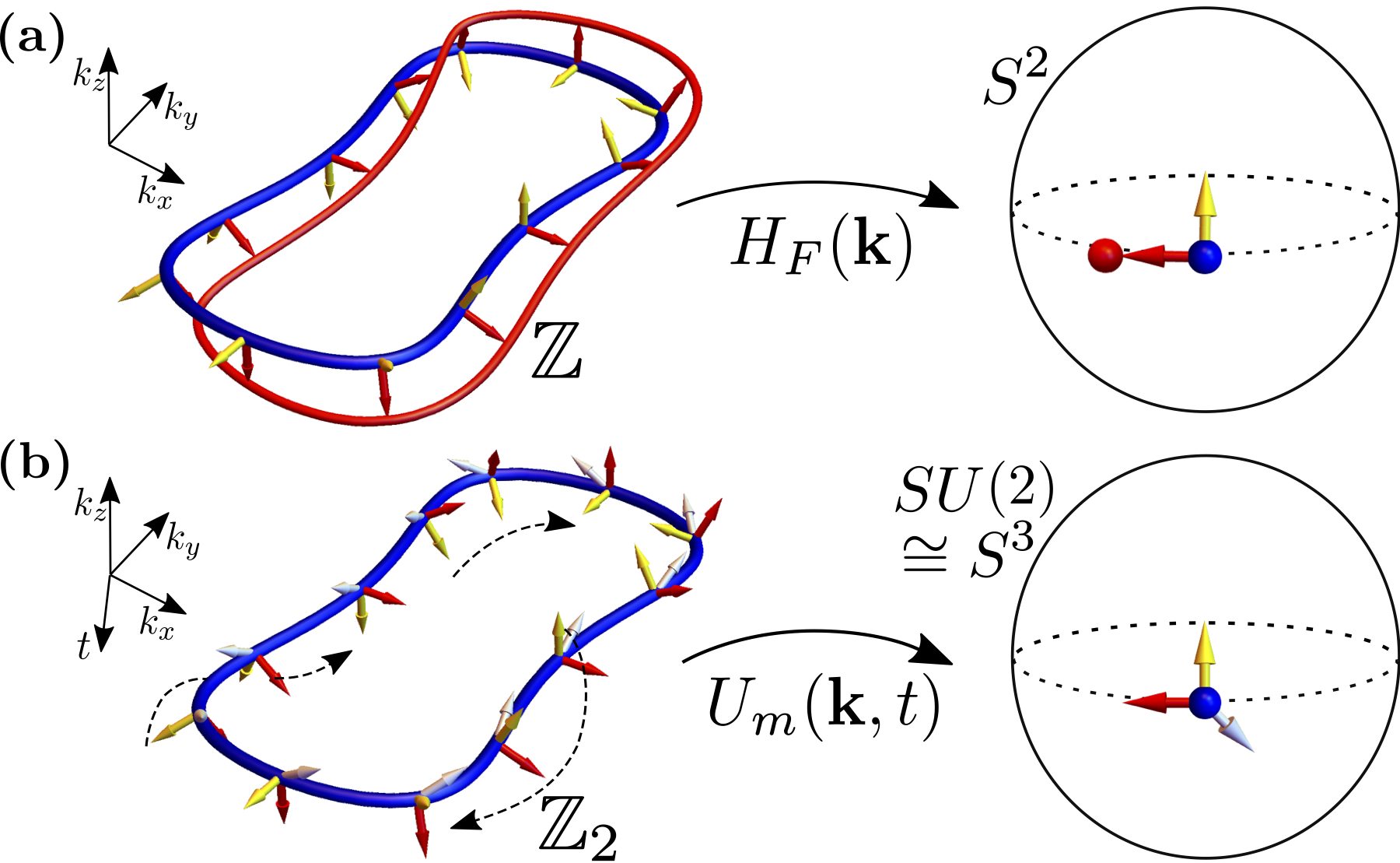In recent years, the classification of topological phases of matter has been extended to periodically driven (Floquet) systems far from equilibrium. Some of the predicted phenomena go beyond what is realizable by static Hamiltonians, including chiral edge states belonging to quasi-energy bulk bands with a vanishing Chern number and topologically protected transport of quantum information. In a recent study, we examined a generalization of the Thouless charge pump, a simple yet fundamental example of topology in quantum systems, to periodically driven systems. We have demonstrated that in the out of equilibrium setting, energy, rather than charge, may undergo quantized pumping. In particular, the energy transported per cycle is quantized in units of the drive frequency leading to the absorption of precisely a single photon. In a different study, we predict the existence of a novel Floquet topological insulator in three-dimensional two-band systems, the Floquet Hopf insulator. Remarkably, its associated Floquet dynamics is classified by an intrinsically Floquet Z2 invariant representing a condensed matter realization of the topology underlying the Witten anomaly in particle physics.
Universal dynamics near quantum criticality
The hallmark of critical phenomena is the emergence of universality, where seemingly microscopically distinct physical systems, such as magnets and superfluids share a common behavior near a continuous phase transition. In the quantum case not only static properties become universal but also the long-time dynamics. To date, quantum critical phenomena have been exemplified in a plethora of experimental systems such as dimerized antiferromagnets, superconducting thin films and cold atomic systems trapped in an optical lattice.
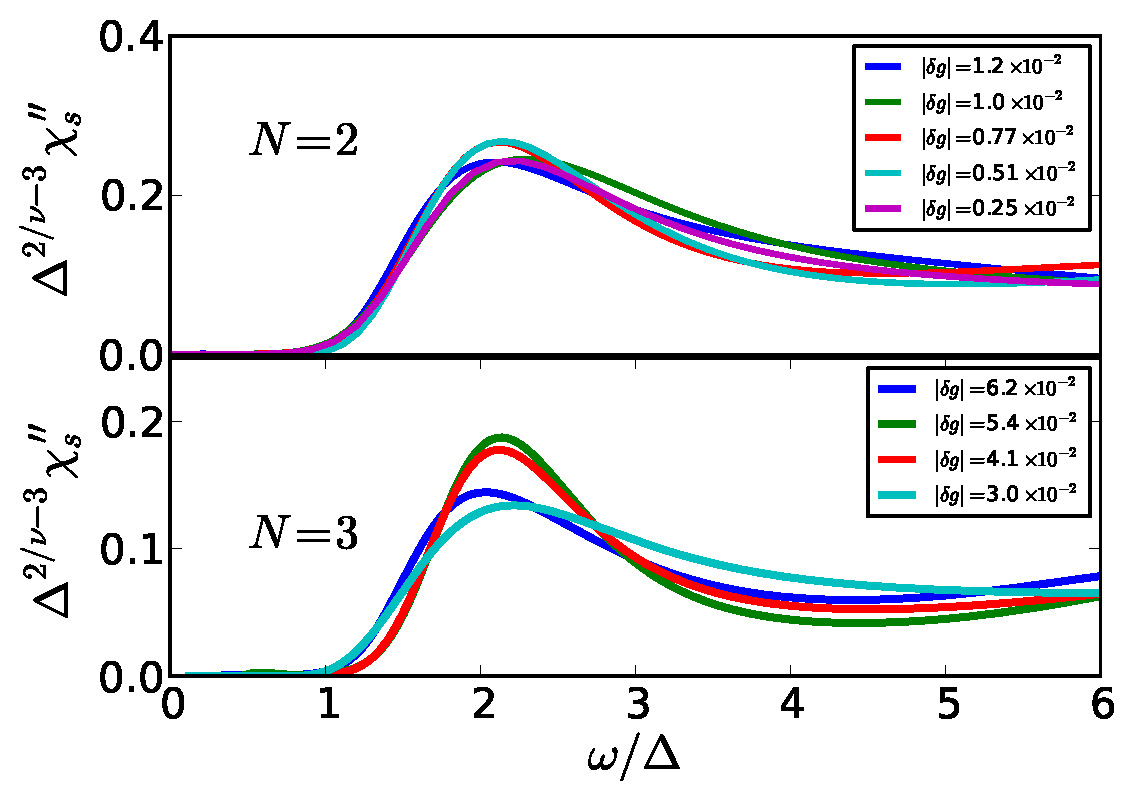
Our main contributions to this research field are: (i) Demonstrating that the Higgs (“amplitude”) mode, which corresponds to fluctuations of the order parameter magnitude in the broken symmetry phase, survives as a sharp resonance arbitrarily close to critically in two spatial dimensions. (ii) Proposing a concrete observable and the first computation of the elusive dual vortex superfluid stiffness. (iii) Presenting new universal scaling relations for the high frequency optical conductivity. These results addressed important open theoretical questions regarding dynamics near quantum criticality and provided concrete predictions that can be probed experimentally.